Maize Genetics Cooperation
Newsletter vol 85 2009
RIO CUARTO, ARGENTINA
Universidad Nacional de R´┐Żo Cuarto
CASTELAR, ARGENTINA
Instituto Nacional de Tecnolog´┐Ża Agropecuaria
Path coefficient
analysis of ´┐ŻMal de R´┐Żo Cuarto´┐Ż disease components.
--Dallo, MD; Iba´┐Żez, MA; Borghi, ML; Girardi, VN;
Bonamico, NC; Salerno, JC; D´┐Żaz, DG; Di Renzo, MA.
INTRODUCTION
The ´┐ŻMal de R´┐Żo Cuarto´┐Ż (MRC) is considered the most important viral
disease of corn in Argentina, causing increase damage and high yield losses to
susceptible cultivars (Lenard´┐Żn, SL et al., Plant Dis 82:448, 1998; Di Renzo, MA,
et al., J Agr Sci
139:47-53, 2002). The disease is caused by MRC virus which belongs to the genus
Fijivirus,
within the family Reoviridae
and is transmitted by the planthopper Delphacodes kuscheli Fennah (Hemiptera: Delphacidae) (Nome, SF et al., Phytopathol
Z 101:7-15, 1981; Ornaghi, JA et al., J Gen Breed
47:227-282, 1993). Its symptomatology depends of the
plant phenological state when it is infected, the
genotype and the environmental conditions where the culture grown. This includes
stunting, short internodes, galls or enations on the abaxial side of the leaves, size reduction and malformation
of spikes, ears and leaves (Lenard´┐Żn, SL et al, SL Lenard´┐Żn Ed., IFFIVE, INTA, JICA, 1999; Di Renzo, MA et al., J Agric Sci
142:289-295, 2004). Since both economic and environmental reasons prevent a
raise in agrochemicals usage, future cereal improvement will rely on germplasm that optimize present genetic tolerance to plant pathogens
(Abeledo, LG et al., Euphytica
130:325-334, 2003). This is an effective way of both increasing and stabilizing
production in affected areas.
Selection for one trait usually affects several traits. The correlated
response to selection is a change in one or more traits due to selection of
another as a result of genetic relations between them. Genetic correlations are
useful to decide on selection strategies since they express the relative
importance of pleiotropy and linkage between loci (Kang,
MS et al., Crop Sci 23:643-647, 1983;
Kang, MS, Applied quantitative genetics. MS Kang Publisher, Baton Rouge, LA,
1994). The genetic correlations can be estimated from phenotypic values, which
are influenced by type of gene action, environmental effects and genotype x
environment interactions (Falconer and Mackay, Introduction to quantitative
genetics. Longman Technical, Essex, UK, 1996).
Nevertheless, while correlation coefficient only measures the
association magnitude between variables, the path coefficient analysis (Wright,
S, J Agric Res 20:557-587, 1921; Wright, S, Ann Math Stat 5:161-215, 1934)
allows dissecting the correlation between them into effects, direct and
indirect. This method has been commonly used in crop breeding studies to
establish the relationships between grain yield and its contributing components
(Mohammadi, SA et al., Crop Sci
43:1690-1697, 2003). In addition, there are many references of its application
in plant pathology studies (Van Bruggen and Arneson, Phytopathology
76:874-878, 1986; Nayak, P et al.,
J Phytopathol 119:312-318, 1987; Neher, DA et al., Plant Dis
77:1106-1111, 1993; Birhman and Singh, Ann Appl Biol 127:353-362, 1995; Desprez-Loustau and Wagner, Eur J
Plant Pathol 103:653-665, 1997; Garcia, D et al., Eur J Forest Pathol 29:323-338,
1999). Therefore, it would be useful to get information regarding direct and
indirect relationships among MRC disease tolerance and different related
traits. The objectives of this work were: i) to
determine phenotypic and genetic correlation coefficients among MRC disease
tolerance and different related traits and ii) to present a path coefficient
analysis to show how these traits affect MRC disease tolerance.
MATERIALS AND METHODS
Plant
material
One hundred and forty
four F2:6 recombinant inbred lines (RIL) were developed from a cross
between Mo17, a susceptible dent line, and BLS14, a partially resistance red
flint line. The RILs were assessed to MRC disease and parental genotypes were
used as controls in each plot.
Field
trials
The RILs were tested during
the 2004 summer cycle in field
experiments at two locations belonging to the endemic area: R´┐Żo Cuarto
(R4) and Sampacho (S4). The field trials were
conducted in a randomized complete block design with two replicates of
single-row plots. Each plot consisted of 3.0 m rows with 0.7 m spacing. Plants were thinned to a distance of 0.15 m in the row. The sowing date
determination was made through insect vector monitoring during spring, in order
to Delphacodes kuscheli
population reach the peak during early stages of maize development.
Symptoms
observed and scored
Disease symptoms were scored 60-70 days after male flowering. Individual
plants from each plot were phenotypically screened
for traits related to MRC disease: plant height (PH), internodes (IN), enations (EN), flag leaf edge (LE), width (LW) and length
(LL), panicle (PA) and ear (EA). A disease severity grade was estimated for each
plant according to a 0 - 3 scale proposed by Ornaghi et al. (Maydica 44:219-223, 1999).
The response variable is the disease severity index (DSI) based on the disease
severity grades of individual plants. DSI was calculated for each plot and used
to rate RIL for their reaction to MRC disease according to Grau
et al. (Plant Dis
66:506–508, 1982). The details of the rating for MRC severity were
described in Di Renzo et al. (J Agr Sci
139:47-53, 2002).
Statistical
analysis
Data from each trial location were subjected to variance and covariance
analyses using the PROC GLM procedure of SAS (SAS Institute ver
9.1.3). Genetic and phenotypic correlation coefficients among DSI and traits
related to MRC disease were determined from variance and covariance components.
The path coefficient analysis was performed to calculate direct and indirect
effects among the response variable, DSI, and MRC related predictor variables.
Direct and indirect path coefficients were calculated as firstly proposed
Wright (J Agric Res 20:557-587, 1921; Ann Math Stat 5:161-215, 1934), and then
Dewey and Lu (Agron J 51:515-518, 1959) and Li (Path
analysis: a primer. Boxwood Press, Pacific Grove, CA, 1975).
For each trait, direct path coefficient was solved by means of PROC IML (SAS
Institute ver 9.1.3). The product of appropriate
correlation coefficient (r) and path
coefficient values provides the indirect path coefficient. Correlations and
path coefficient analyses based on genetic values define more precisely what
factors affect DSI genetically. Previous to analysis, the original data was
logarithmically transformed to satisfy the assumption of additivity
among the components. The presence of multicollinearity
among variables was measured using the variance inflation factor (VIF) and the
condition number (CN). Residual effects and determination coefficients were
estimated according to Kang (Applied quantitative genetics. MS Kang Publisher,
Baton Rouge, LA, 1994). The criterion followed to evaluate the extent of
effects of MRC related traits on DSI magnitude was according to Board et al. (Crop Sci
37:879-884, 1997).
RESULTS AND DISCUSSIONS
Phenotypic and genetic correlations coefficients among all pairs of
traits are shown in Table 1. In general, phenotypic and genetic correlation
coefficients agreed in sign and the magnitude of the phenotypic correlation
coefficient was practically the same that the genetic correlation coefficient
indicating that the influence of environment on these relationships was little
or negligible. However, in most cases, the genetic correlation estimates
between DSI and MRC disease related traits were slightly high showing that they
are genetically associated or that they are physiologically related (Sidwell, RJ et al., Crop Sci 16:650-654, 1976). At R4 location, EN had the highest
positive phenotypic correlation on DSI (0.94) followed by IN (0.91) and EA
(0.64) but, IN had the highest positive genetic correlation on DSI (0.96)
followed by EN (0.95) and EA (0.69). However at S4 environment, both phenotypic
and genetic correlation coefficient of EN on DSI showed the highest positive
values (0.96 and 0.98, respectively) followed by IN (0.90 and 0.94,
respectively) and PA (0.69 and 0.77, respectively).
|
Table 1. Phenotypic and genetic correlations
among all pairs of traits at R4 and S4 environments. |
||||||||||||||||
|
|
PA |
LL |
LW |
LE |
EN |
IN |
EA |
DSI |
||||||||
|
PA |
|
|
0.490 0.535 |
|
0.408 0.399 |
|
0.237 0.225 |
|
0.576 0.596 |
++ |
0.552 0.581 |
|
0.255 0.298 |
|
0.591 0.611 |
++ |
|
|
|
|
|
|
|
|
|
|
||||||||
|
LL |
0.577 0.703 |
|
|
|
0.411 0.412 |
|
0.175 0.128 |
|
0.353 0.358 |
|
0.309 0.363 |
++ |
0.019 0.002 |
|
0.352 0.375 |
++ |
|
|
|
|
|
|
|
|
|
|
||||||||
|
LW |
0.444 0.320 |
|
0.362 0.340 |
|
|
|
0.119 0.042 |
|
0.155 0.092 |
|
0.148 0.137 |
|
-0.044 -0.143 |
|
0.189 0.166 |
|
|
|
|
|
|
|
|
|
++ |
|
||||||||
|
LE |
0.324 0.350 |
|
0.480 0.530 |
++ |
0.128 -0.038 |
|
|
|
0.534 0.558 |
|
0.518 0.582 |
++ |
0.596 0.679 |
++ |
0.541 0.556 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
EN |
0.666 0.762 |
|
0.622 0.747 |
++ |
0.226 0.243 |
|
0.566 0.714 |
|
|
|
0.867 0.913 |
++ |
0.600 0.648 |
++ |
0.937 0.955 |
++ |
|
|
|
|
|
|
|
++ |
|
|
||||||||
|
IN |
0.616 0.697 |
++ |
0.530 0.646 |
|
0.212 0.221 |
|
0.483 0.603 |
|
0.849 0.891 |
++ |
|
|
0.559 0.651 |
++ |
0.914 0.961 |
++ |
|
|
|
|
|
++ |
|
|
|
|
||||||||
|
EA |
0.427 0.469 |
|
0.233 0.272 |
|
0.049 -0.016 |
|
0.282 0.331 |
++ |
0.528 0.600 |
|
0.486 0.570 |
|
|
|
0.642 0.691 |
++ |
|
|
|
|
|
|
|
|
|
|
||||||||
|
DSI |
0.685 0.774 |
++ |
0.597 0.707 |
++ |
0.232 0.240 |
|
0.532 0.660 |
|
0.961 0.979 |
++ |
0.898 0.941 |
++ |
0.549 0.628 |
++ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
´┐Ż R4 = R´┐Żo Cuarto 2004; S4 = Sampacho. DSI = disease
severity index; PA = panicle; LL = leaf lenght; LW
= leaf width; LE = leaf edge; EN = e-nations; IN = internodes; EA = ear. ++, +
Significant at the 0.01 and 0.05 levels, respectively, by bootstrap method. ´┐Ż Values
above/below the diagonal: correlations among all pairs of traits at R4 and S4
environments, respectively. Genetic values are shown in bold. |
||||||||||||||||
Fig. 1. Path diagram showing causal
relationships between disease severity index (DSI) and Mal de R´┐Żo Cuarto
(MRC) disease related traits. One-headed arrow represents direct paths and
double-headed arrows represent correlations (r).
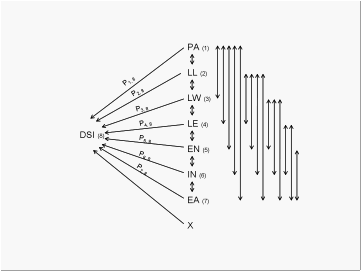
Because of the similarity between phenotypic and genetic correlations,
the phenotypic and genetic path coefficients were also quite similar. The path
diagram based both phenotypic and genetic correlation coefficients were carried
out according to shown in Fig. 1. The almost equal magnitude of EN and IN
direct effects on DSI at both phenotypic and genetic levels indicated that
these effects were under genetic control with unimportant environmental
effects. However, at R4 and S4 environments, the genetic direct effects of EN
and IN increased hardly over their respective phenotypic direct effects which
suggest a negative relationship between DSI and environmental effects. In
general, EN and IN were the primary and secondary direct determinants of DSI
over both environments at the phenotypic and genetic levels (Table 2).
Nevertheless, at R4 location, IN showed the highest positive genetic direct
effect on DSI (0.490) followed by EN (0.445). Similarly, the large positive
phenotypic and genetic direct effects of EN and IN on DSI was counterbalanced by
a small phenotypic and genetic indirect effects via the remaining traits
included in the analysis. In most cases, the remaining traits had negligible
phenotypic and genetic direct effects but the phenotypic and genetic indirect
effects were intermediate via EN and IN on both environments (Table 2).
Table 2. Phenotypic and genetic path
coefficient analysis of DSI and MRC components at R4 and S4 environments. |
||||
|
Pathway |
R4 |
S4 |
||
|
DSI vs. PA |
|
|
|
|
|
Direct effect |
0.032 |
-0.010 |
0.052 |
0.053 |
|
Indirect effect via |
|
|
|
|
|
LL |
0.012 |
0.011 |
-0.004 |
-0.032 |
|
LW |
0.016 |
0.032 |
-0.001 |
0.000 |
|
LE |
-0.005 |
-0.020 |
-0.004 |
-0.011 |
|
EN |
0.290 |
0.266 |
0.454 |
0.532 |
|
IN |
0.213 |
0.285 |
0.173 |
0.219 |
|
EA |
0.033 |
0.047 |
0.016 |
0.013 |
|
Correlation |
0.591 |
0.611 |
0.685 |
0.774 |
|
DSI vs. LL |
|
|
|
|
|
Direct effect |
0.025 |
0.021 |
-0.007 |
-0.046 |
|
Indirect effect via |
|
|
|
|
|
PA |
0.016 |
-0.005 |
0.030 |
0.038 |
|
LW |
0.016 |
0.033 |
-0.001 |
0.000 |
|
LE |
-0.004 |
-0.011 |
-0.007 |
-0.017 |
|
EN |
0.178 |
0.159 |
0.424 |
0.522 |
|
IN |
0.119 |
0.178 |
0.149 |
0.203 |
|
EA |
0.003 |
0.000 |
0.008 |
0.007 |
|
Correlation |
0.352 |
0.375 |
0.597 |
0.707 |
|
DSI vs. LW |
|
|
|
|
|
Direct effect |
0.038 |
0.080 |
-0.002 |
-0.001 |
|
Indirect effect via |
|
|
|
|
|
PA |
0.013 |
-0.004 |
0.023 |
0.017 |
|
LL |
0.010 |
0.009 |
-0.002 |
-0.016 |
|
LE |
-0.003 |
-0.004 |
-0.002 |
0.001 |
|
EN |
0.078 |
0.041 |
0.154 |
0.169 |
|
IN |
0.057 |
0.067 |
0.060 |
0.070 |
|
EA |
-0.006 |
-0.023 |
0.002 |
0.000 |
|
Correlation |
0.189 |
0.166 |
0.232 |
0.240 |
|
DSI vs. LE |
|
|
|
|
|
Direct effect |
-0.022 |
-0.089 |
-0.014 |
-0.031 |
|
Indirect effect via |
|
|
|
|
|
PA |
0.008 |
-0.002 |
0.017 |
0.019 |
|
LL |
0.004 |
0.003 |
-0.003 |
-0.024 |
|
LW |
0.005 |
0.003 |
0.000 |
0.000 |
|
EN |
0.269 |
0.249 |
0.386 |
0.498 |
|
IN |
0.200 |
0.285 |
0.136 |
0.190 |
|
EA |
0.077 |
0.108 |
0.010 |
0.009 |
|
Correlation |
0.541 |
0.556 |
0.532 |
0.660 |
|
DSI vs. EN |
|
|
|
|
|
Direct effect |
0.504 |
0.445 |
0.681 |
0.698 |
|
Indirect effect via |
|
|
|
|
|
PA |
0.019 |
-0.006 |
0.035 |
0.041 |
|
LL |
0.009 |
0.008 |
-0.004 |
-0.034 |
|
LW |
0.006 |
0.007 |
-0.001 |
0.000 |
|
LE |
-0.012 |
-0.049 |
-0.008 |
-0.022 |
|
IN |
0.334 |
0.447 |
0.238 |
0.280 |
|
EA |
0.078 |
0.103 |
0.019 |
0.016 |
|
Correlation |
0.937 |
0.955 |
0.961 |
0.979 |
|
DSI vs. IN |
|
|
|
|
|
Direct effect |
0.385 |
0.490 |
0.281 |
0.315 |
|
Indirect effect via |
|
|
|
|
|
PA |
0.018 |
-0.006 |
0.032 |
0.037 |
|
LL |
0.008 |
0.008 |
-0.003 |
-0.030 |
|
LW |
0.006 |
0.011 |
0.000 |
0.000 |
|
LE |
-0.011 |
-0.052 |
-0.007 |
-0.019 |
|
EN |
0.436 |
0.407 |
0.578 |
0.622 |
|
EA |
0.073 |
0.103 |
0.018 |
0.016 |
|
Correlation |
0.914 |
0.961 |
0.898 |
0.941 |
|
DSI vs. EA |
|
|
|
|
|
Direct effect |
0.130 |
0.158 |
0.036 |
0.027 |
|
Indirect effect via |
|
|
|
|
|
PA |
0.008 |
-0.003 |
0.022 |
0.025 |
|
LL |
0.000 |
0.000 |
-0.002 |
-0.012 |
|
LW |
-0.002 |
-0.011 |
0.000 |
0.000 |
|
LE |
-0.013 |
-0.060 |
-0.004 |
-0.010 |
|
EN |
0.302 |
0.288 |
0.359 |
0.419 |
|
IN |
0.215 |
0.319 |
0.137 |
0.179 |
|
Correlation |
0.642 |
0.691 |
0.549 |
0.628 |
|
Coefficient of
determination |
0.931 |
0.971 |
0.951 |
0.985 |
|
Residual effect |
0.262 |
0.170 |
0.222 |
0.123 |
|
´┐Ż R4 = R´┐Żo Cuarto 2004; S4 = Sampacho.
DSI = disease severity index; PA = panicle; LL
= leaf lenght; LW = leaf width; LE = leaf edge; EN
= enations; IN = internodes; EA = ear. ´┐Ż
Genetic values are shown in bold. |
||||
The phenotypic and genetic path coefficients for DSI accounted for a
large proportion of phenotypic and genetic variation on both environments as
indicated by a large coefficient of determination and by the corresponding
small residual effect. In the phenotypic and genetic path analysis, the
residual effect represents the failure of the estimated genetic correlations
among the variables to account for the total genetic variation in a trait (Sidwell, RJ et al., Crop Sci
16:650-654, 1976).
The most important components of DSI, if we just consider phenotypic and
genetic correlation coefficients, were EN, IN, EA, PA and LE. Nevertheless,
phenotypic and genetic path coefficient analysis showed that among these traits
only EN and IN were the most important to increase DSI. The direct effects of
EA, PA and LE were little or negligible. The results of this study suggest that
EN and IN are the best traits in determining DSI on both environments and may
be useful as an indirect selection criteria in breeding and selection programs
related to MRC disease.
REFERENCES
Abeledo,
L.G., D.F. Calderini and G.A. Slafer.
2003. Genetic improvement of barley yield potential and its physiological
determinants in Argentina (1944-1998). Euphytica 130:
325-334.
Birhman,
R.K. and B.P. Singh. 1995. Path-coefficient analyses and genetic parameters of
the components of field resistance of potatoes to late blight. Ann Appl Biol. 127: 353-362.
Board, J.E., M.S. Kang and
B.G. Harville. 1997. Path analyses
identify indirect selection criteria for yield of late-planted soybean. Crop
Sci. 37: 879-884.
Desprez-Loustau, M.L. and K. Wagner.
1997. Components of maritime pine susceptibility to twisting rust – A
path coefficient analysis. Eur J Plant Pathol. 103: 653-665.
Dewey, D.R. and K.H. Lu. 1959. Correlation and
path coefficient analysis of components of crested wheat grass seed production.
Agron J. 51: 515-518.
Di Renzo, M.A., N.C. Bonamico, D.D. D´┐Żaz, J.C.
Salerno, M.A. Iba´┐Żez and J.J. Gesumaria.
2002. Inheritance of resistance to Mal de R´┐Żo Cuarto (MRC) disease in Zea mays (L.). J Agr Sci. 139: 47-53.
Di Renzo, M.A., N.C. Bonamico, D.D. D´┐Żaz, M.A. Iba´┐Żez, M.E. Faricelli, M.G. Balzarini and J.C. Salerno. 2004. Microsatellite markers
linked to QTL for resistance to Mal de R´┐Żo Cuarto disease in Zea mays (L.). J
Agric Sci. 142: 289-295.
Falconer, D.S. and T.F.C.
Mackay. 1996. Introduction to quantitative genetics, 4th
ed. Longman Technical, Essex, UK.
Garcia, D., V. Troispoux, N. Grange, F. Rivano
and J. D'Auzac. 1999. Evaluation of
the resistance of 36 Hevea
clones to Microcyclus ulei and
relation to their capacity to accumulate scopoletin
and lignins. Eur J Forest Pathol. 29: 323-338.
Grau,
C.R., V.L. Radke and F.L. Gillespie. 1982. Resistance
of soybean cultivars to Sclerotinia sclerotiorum.
Plant Dis. 66: 506–508.
Kang, M.S., J.D. Miller and P.Y.P. Tai. 1983.
Genetic and phenotypic path analyses and heritability in sugarcane. Crop Sci.
23: 643-647.
Kang, M.S. 1994. Applied
quantitative genetics. M.S. Kang Publisher, Baton Rouge, LA.
Lenard´┐Żn,
S.L., G.J. March, S.F. Nome and J.A. Ornaghi. 1998.
Recent outbreak of ´┐ŻMal de R´┐Żo Cuarto Virus´┐Ż on corn in Argentina. Plant Dis 82: 448.
Lenard´┐Żn,
S.L., G.J. March y J.A. Ornaghi, 1999. Virus del Mal de
R´┐Żo Cuarto en ma´┐Żz. En: Lenard´┐Żn, S.L. (Ed.). Enfermedades causadas por virus y
fitoplasmas en cultivos extensivos intensivos. Proyecto de Investigaciones en
Fitovirolog´┐Ża. IFFIVE, INTA, JICA. Hoja Informativa. Ma´┐Żz
N´┐Ż 2, 10 pp.
Li, C.C. 1975. Path analysis: a primer, 3rd
ed. Boxwood Press, Pacific Grove, CA.
Mohammadi, S.A., B.M. Prasanna and
N.N. Singh. 2003. Sequential path model for determining
interrelationships among grain yield and related characters in maize. Crop Sci.
43: 1690-1697.
Nayak,
P.,
A.V. Suriya Rao and N.K. Chakrabarti. 1987. Components of resistance to bacterial
blight disease of rice. J Phytopathol. 119: 312-318.
Neher,
D.A., C.D. McKeen and J.M. Duniway.
1993. Relationships among phytophthora root rot
development, P. parasitica
populations in soil, and yield of tomatoes under commercial field conditions.
Plant Dis. 77: 1106-1111.
Nome, S.F., S.L. Lenard´┐Żn,
B.C. Raju, I.G. Laguna, S.K. Lowe and D. Docampo. 1981. Association of reovirus-like
particles with ´┐ŻEnfermedad de R´┐Żo IV´┐Ż of maize in
Argentina. Phytopathol Z. 101: 7-15.
Ornaghi,
J.A., G.T. Boito, G. Sanchez, G.J. March and J.E. Beviacqua.
1993. Studies on the population of Delphacodes kuscheli Fennah in different
years and agricultural areas. J Gen Breed. 47: 227-282.
Ornaghi,
J.A., G.J. March, G.T. Boito, A. Marinelli, J.E. Beviacqua, J. Giuggia and S.L. Lenard´┐Żn. 1999. Infectivity in natural populations of Delphacodes kuscheli
vector of ´┐ŻMal de R´┐Żo Cuarto´┐Ż virus. Maydica 44:
219-223.
SAS Institute Inc. 2005.
SAS/STAT user´┐Żs guide, Version 9.1.3. SAS Institute
Inc., Cary, NC.
Sidwell,
R.J., E.L. Smith and R.W. McNew. 1976. Inheritance
and interrelationships of grain yield and selected yield-related traits in a
hard red winter wheat cross. Crop Sci. 16: 650-654.
Van Bruggen, A.H.C.
and P.A. Arneson. 1986. Path coefficient analysis of
effects of Rhizoctonia solani on
growth and development of dry beans. Phytopathology
76: 874-878.
Wright, S. 1921. Correlation
and causation. J Agric Res. 20: 557-587.
Wright, S. 1934. The method of
path coefficients. Ann Math Stat. 5: 161-215.
Please Note: Notes submitted to the Maize Genetics
Cooperation Newsletter may be cited only with consent of authors.