Maize Genetics Cooperation
Newsletter vol 84 2010
Please Note: Notes submitted to the Maize
Genetics Cooperation Newsletter may be cited only with consent of authors.
ROSARIO, ARGENTINA.
Facultad de Ciencias
Exactas, Ingenier�a y Agrimensura - UNR.
Centro Internacional Franco Argentino de Ciencias de la
Informaci�n y de Sistemas - CONICET
Application of error correcting codes for heterotic group assignation.
--Ornella,
L; Tapia, E
Introduction of exotic maize (Zea mays L.) into breeding programs may enhance genetic variability and lead
to greater progress from selection.
However, the pool of available exotic germplasm is large and diverse,
making choices of potential parents difficult. Two major heterotic
group-classification methods are currently used widely across the world. The
traditional method uses specific combining ability with some line-pedigree
information and/or field hybrid-yield information to assign a maize line to a
heterotic group (Hallauer and Miranda, Quantitative Genetics in Maize Breeding,
2nd ed. Iowa State Univ. Press, Ames, IA, 1988).
Another method employs various molecular markers to compute genetic similarity
(GS) or genetic distance (GD) in order to assign maize lines to different
heterotic groups (Mohammadi and
Prasanna, Crop Sci. 43:1235–1248, 2003). However, the results of
these associations are still inconsistent (dos Santos Dias et al., Genet. Mol.
Res. 3: 356-368, 2004).
Machine learning is an emerging scientific discipline concerned with the
design and development of algorithms that allow computers
to change behavior based on data, such as from sensor data or databases
(Witten and Eibe, Data Mining: Practical Machine Learning Tools and Techniques,
2nd ed. Morgan Kaufmann, San
Francisco, 2005). In particular, supervised learning algorithms allows for
deducing a function from training data. The training data
consist of pairs of input objects (typically vectors of features) and desired
outputs i.e. the class (Witten and Eibe, 2005).
We conjecture that traditional distance-based methods currently
available do not capture the non-linear relationship between parental molecular
data and progeny performance and that such hindrance can be overcome by
supervised learning algorithms. Among them, support vector machines (SVMs) have
shown high generalization abilities and have become very popular in the last
few years (Rifkin and Klautau, JMLR 5:101-114, 2004). However, they are binary
classifiers and a combination scheme is necessary to extend SVMs for problems
with more two classes (Rifkin and Klautau, JMLR 5:101-114, 2004). In this work
we explore the performance of the recently introduced class of ECOC-SVM (Error
Correcting Output Coding-Support Vector Machine) classifiers, based on
recursive error correcting codes of communication theory (Tapia et al., LNCS
3541:108–117, 2005), in heterotic group assignation. As a control we used
four (4) Native multiclass classifiers: Naive Bayes (John and Langley, 11th Conf.
on Uncertainty in A, 338–345, 1995), Bayes Network
(Friedman et al., Mach Learn. 29:131–163, 1997), Decision Tree J48
(Quinlan, C4.5: Programs for Machine Learning. Morgan Kaufmann Publishers, San
Mateo, CA., 1993) and Logistic Model Trees or just Simple Logistic (Landwehr et
al., Mach Learn. 161–205, 2005). We also report the performance of the ensemble method using
as a base classifier Naive Bayes and J48 (Witten and Eibe, 2005).
Classifiers were evaluated with two datasets: Morales dataset, involving
26 inbreeds of temperate germplasm clustered into four heterotic groups by
topcross (Eyherabide et al., Plant Breeding: The Arnel R. Hallauer
International Symposium, Blackwell Publishing, pp. 352–379, 2006) and
characterized by 42 attributes derived from 21 microsatellites (MNL 79:36-37,
2005); and Xia dataset, comprising
73 inbreeds of tropical germplasm clustered in 8 heterotic groups and
characterized by 166 attributes
derived from 83 microsatellites (Xia et al., Crop Sci. 4:2230-2237, 2004).
The decomposition method of ECOC employs a binary matrix of order 
to convert a k-multiclass problem into n binary tasks (
) (Dietterich and Bakiri, JAIR 2:263-286,
1995); this allows us to explore the performance of matrices with n = [2,3,�, 7] for Morales Data, and n = [3, 16, 29,� , 120 ] for Xia data.
The predictive power of proposed algorithms was evaluated by means of Cohen�s
Kappa coefficient (Landis and Koch, Biometrics 33: 159–174, 1977) exhibited
across 30 Montecarlo runs of stratified 10-Fold Cross Validation (CV)
experiments (Kirchner et al., Comput
Electron Agric. 42:111–127.2004). The choice of the Kappa coefficient was
motivated by its ability to better measure the agreement between binary
inter-annotators than the traditional error rate. The former takes into account
chance agreements and it is well suited for unequal class distribution datasets
then traditional error rate (Kirchner et al., 2004).
Figures 1 and 2 show the performance of the 7 classifiers on Morales and
Xia dataset respectively.
Results of ECOC codes corresponds to kappa values obtained with codes
that, with the lowest number of columns reached the best kappa value (n = 55
for Xia Data and n = 7 for Morales data).
Although some statistical test is needed in order to support the
significance of the better or poorer performance of classifiers, it can be seen
from visual inspection of both boxplots that ensembles (ECOC codes) outperform
the performance of most native classifiers. The only exception is simple
logistic, which outperforms ECOC-SMO ensemble in Morales data; however it
remains to explore the optimizations of SVM parameters, which is reported to
significantly improve the final performance of the ensemble (Rifkin and Klautau,
2004).
It is reported that the aim of the classifier ensembles is to take
advantage of the individual classifiers� capabilities by selecting or weighting
their individual decisions (Dietterich, LNCS 1857: 1-15, 2000). It also can be
seen from both boxplots that ensembles (ECOC codes) of Decision tree and Na�ve
Bayes did improve the performance of the single classifier (Figs 1 and 2).
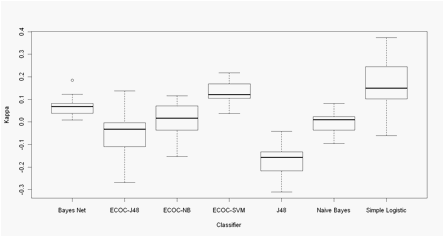
Figure 1- Morales data. Boxplots of the Cohen�s Kappa coefficient in 30
Montecarlo runs of 10-Fold CV experiments.
ECOC - xx Error correcting
output code + base classifier: NB -
Na�ve Bayes, SVM - Support vector machine, J48 -Decision Tree J48.
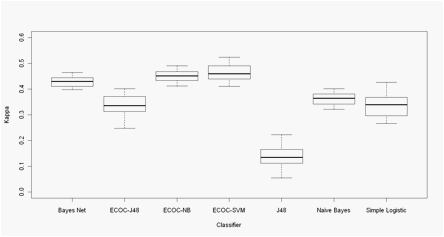
Figure 2- Xia data. Boxplots of the Cohen�s Kappa coefficient in 30
Montecarlo runs of 10-Fold CV experiments.
ECOC - xx Error correcting
output code + base classifier: NB -
Na�ve Bayes, SVM - Support vector machine, J48 -Decision Tree J48.
Finally, although results obtained do not allow molecular markers to replace field essays (top cross or diallel) in heterotic group assignment[1], there is strong evidence that using data with more training instances could generate successful classifiers. Moreover, the potential impact, in time and money, on crop sustainability makes our research worth to try: while traditional genetic breeding requires expensive fields test and a time scale in the order of years for obtaining an heterotic assignment, in our proposed framework costs are significantly lower and the time scale is in the order of weeks, two weeks for growing an small plant plus a week to obtain molecular data and a couple of days for computational analysis.